Reinforcement Learning(1)

13기 이재빈

과제 내용

논문 리뷰: 'Playing Atari with Deep Reinforcement Learning'

우수과제 선정이유

강의중에 설명이 부족했던 개념들(e-greedy, off-policy 등)을 따로 찾아서 명료하게 정리해 주셔서 다른 분들에게 많은 참고가 될 것 같아서 선정하였습니다.

Atari2006은 Reinforcement Learning에 Deep Learning을 접목시켜, 사람이 플레이하는 수준으로 구현해 낸 learning algorithm입니다. model = CNN + Q-Learning

Deep Learning을 그대로 RL에 적용시키기에는 몇 가지 문제가 발생합니다.

  1. data의 Label이 존재하지 않습니다

    • RL은 (sparse, noisy, delayed) 특성을 가진 scalar reward로부터 학습합니다

  2. 데이터가 iid를 따르지 않습니다 (highly correlated)

    • RL은 time series data이기 때문에, sequence들 끼리 높은 상관관계를 가지고 있습니다

  3. 일정한 분포를 따르지 않습니다 (non-stationary dist)

    • RL의 algorithm은 새로운 behavior를 계속적으로 학습합니다

.

따라서 여기 논문에서는, 다음과 같은 사항들을 통해 딥러닝과 강화학습을 접목시켰습니다.

CNN +) Q-Learning +) replay mechanism

ε \varepsilon (environment) = Atari emulator 구성 요소: actions, observations(화면), rewards(점수)

  1. ata_t를 선택합니다

  2. 선택한 action은 emulator에게 전달됩니다

  3. state & score를 수정합니다

  4. rt r_t (game score)를 찾습니다

  • 이 때, 현재 상황을 주어진 xt x_t (time t에서의 pixel 값)로만 판단하기에는 무리가 있습니다. 따라서 action, observation을 보고 난 후에 game 전략을 학습합니다.

  • 또한 게임은 언젠가 끝날 것이기 때문에, emulator의 학습 과정은 종결될 것이라고(finite) 가정하고, finite MDP(Markov Decision Process) 로 model을 가정합니다.

우리의 목표는 agent가 emulator와 상호작용하여, future reward를 최대화하는 적절한 action을 선택하는 것입니다. 이를 위해, 다음과 같이 정의합니다.

  • Reward Function Rt=∑t′=tTγ(t′−t)rt{R_t = \sum_{t'=t}^{T} \gamma^(t'-t)r_t} (T T = 종식 시간)

  • Q-function ( $${Q^*}.$$, Optimal action-value function) $Q^*(s,a) = \max_{\pi}\mathbb{E}[R_t|s_t=s, a_t=a, \pi]$ ($\pi$ = policy)

(1) Q-function은 Bellman equation을 따르게 됩니다.

  • $Q^*(s,a) = \mathbb{E}_{s'~ \varepsilon}[r + \gamma\max_{a'}Q^*(s,a)|s,a]$

  • 위의 식에서, expected value를 최대화하는 $a'$ 값을 선택하게 됩니다

  • value iteration 혹은 policy iteration 과정을 거치면서, action-value function을 최적화 하게 됩니다.

(2) Q-Network는 Q-function을 modeling한 network이며, $Q(s,a;\theta)$ ≃ $Q^*(s,a)$입니다. (Freeze target Q-network)

  1. 최적화

    • 최적화의 경우, 보통 linear로 실행되며

    • Neural Network처럼 non-linear로 실행되는 경우도 있습니다. ($\theta$ = weights)

    • Q-Network는 loss function인 $L_i(\theta_i)$ 를 최소화 하기 위한 방향으로 업데이트 됩니다. .

  2. behavior distribution

    • $\rho(s,a)$는 s, a의 probability distribution 입니다.

  3. model-free

    • MDP의 model에 관계없이 optimal policy를 구하는 방법입니다.

    • $\varepsilon$을 정확하게 알고 구하는 것이 아니라, $\varepsilon$에서 sampling 하여 action을 취해보고 정책 함수를 선정합니다.

  4. off-policy

    • 두 가지 policy를 동시에 사용할 경우를 말합니다.

    • learning에 사용되는 policy는 greedy하기 improve를 하고

    • 움직일 때는 현재의 Q function을 토대로 $\varepsilon$-greedy하게 움직입니다.

    • +) behavior policy $\mu$을 $\varepsilon$-greedy로, target policy $\pi$를 greedy로 택하게 됩니다.

cf) on-policy vs off-policy

  1. On-policy: 학습하는 policy와 행동하는 policy가 반드시 같아야만 학습이 가능한 RL 알고리즘

    • ex) SARSA

    • On-policy의 경우 한번이라도 학습을 해서 policy imporvement를 시킨 순간, 그 policy가 했던 과거의 experience들은 모두 사용이 불가능합니다.

    • 한 번 exploration을 해서 얻은 experience를 학습하고 나면 바로 재사용은 불가능합니다.

    • 따라서, 매우 데이터 효율성이 떨어집니다.

  2. Off-policy: 학습하는 policy와 행동하는 policy가 반드시 같지 않아도 학습이 가능한 RL 알고리즘

    • ex) Q-Learning

    • Off-policy는 현재 학습하는 policy가 과거에 했던 experience도 학습에 사용이 가능하고,

    • 사람이나 다른 agent들을 통해서도 학습이 가능합니다.

    • exploration을 계속하면서도 optimal한 policy를 학습할 수 있습니다.

    • 하나의 policy를 따르면서도 multiple policy를 학습할 수 있습니다.

cf) $\varepsilon$-greedy

  1. greedy

    • 한 번 exploration 한 후, 최고의 보상을 받을 수 있는 action을 계속 취하는 것

    • ex) 한 번 플레이 한 후, 돈을 가장 많이 딴 슬롯머신에 모두 투자

    • 수렴은 빠르지만, 충분한 탐험을 하지 않았기 때문에 local minimum에 빠질 가능성이 있습니다.

  2. $\varepsilon$-greedy

    • greedy strategy를 따르는 action을 취할 확률: $1-\varepsilon$

    • random action을 취할 확률: $\varepsilon$

    • ex) 동전을 던져서 윗면이 나오면 점수 좋았던 슬롯머신, 뒷면이 나오면 랜덤으로 선택

TD-gammon

  1. model-free

  2. value function을 MLP (with one hidden layer)로 계산합니다.

  3. backgammon에서만 적용될 수도 있다는 한계가 있습니다.

  4. Diverge : Q-Learning & non-linear function approximators일 때, 발산 가능성이 존재합니다. 수렴성 을 보장하기 위해서는 linear function approximator & better guarantees 필요합니다.

Deep Learning + 강화학습 ?

  • $\varepsilon$: Deep Neural Network

  • Value Function, policy: Boltzmann machines

  • divergence: gradient temporal-difference (nonlinear function approximator, restricted variant)

NFQ: Neural fitted Q-Learning

  • RPROP 알고리즘

  • batch update: 많은 computational cost가 발생합니다.

  • autoencoder: 저차원으로 데이터로 시작하는 것이 raw visual input을 사용하는 것 보다 좋은 결과를 보입니다.

. 따라서... Atari2600에 다음과 같은 사항을 적용시켜 비교해 보게 됩니다.

  • standard RL with linear function approximation & generic visual features

  • a large number of features -> low-dimentional space

  • HyperNEAT evolutionary architecture

  • trained repeatedly

Deep Reinforcement Learning

experience replay

  • 위와 같이 세팅한 Deep RL에는 reward와 Q-value 값이 엄청나게 커질 수 있기 때문에 stable한 SGD 업데이트가 어려워진다는 단점이 있습니다.

  • 또한 on-policy sample을 통해 update하게 되면 sample에 대한 의존성이 커져서 policy가 수렴하지 못하고 진동할 수 있습니다.

  • 이를 해결하기 위한 논문의 핵심 idea가 experience replay 입니다.

  1. each time step마다 agent의 experience를 저장합니다.

    • $e_t = (s_t, a_t, r_t, s_{t+1})$ (experience)

    • $D = e_1, ... , e_N$ (튜플 형태로 마지막 N개 데이터 저장)

    • replay memory

  2. sample을 업데이트 합니다.

    • Q-learning updates, minibatch updates

  3. experience replay가 끝난 후, $\varepsilon$-greedy policy를 사용해 action을 선택합니다.

.

experience replay를 수행함으로써,

  • behavior distribution은 이전 state들의 평균을 기반으로 한 분포를 사용하게 됩니다.

  • 따라서 학습을 smoothing out 할 수 있으며,

  • 진동하거나 발산하는 가능성을 방지해 줍니다.

Deep Q-Learning

  1. data efficiency: 모든 experience들이 weight update 되는 데에 계속 reuse 되기 때문에, experience로 weight update를 한 번만 진행하는 것 보다 훨씬 효율적입니다.

  2. break correlation 데이터 특성 상 연속적인 sample끼리는 corr이 강합니다. ramdom하게 sample을 뽑아 minibatch로 구성하기 때문에, update들의 variance를 줄일 수 있습니다.

  3. determine next samples 다음 training을 위한 data sample을 어느 정도 결정할 수 있습니다. 예를 들어 지금 왼쪽으로 가도록 action을 고른다면, 다음 sample들은 왼쪽에 있는 sample들이 주로 나올 것이라고 예측할 수 있습니다. 따라서 현재 action을 고려하여 효율적으로 뽑을 수 있습니다.

(주의점: off-policy로 학습해야 합니다.)

Preprocessing

  • gray-scale & down-sampling (110* 84)

  • GPU 환경에 맞게 square로 crop 합니다

  • last 4 frame을 stack으로 쌓아서, $\phi$의 input data로 넣습니다.

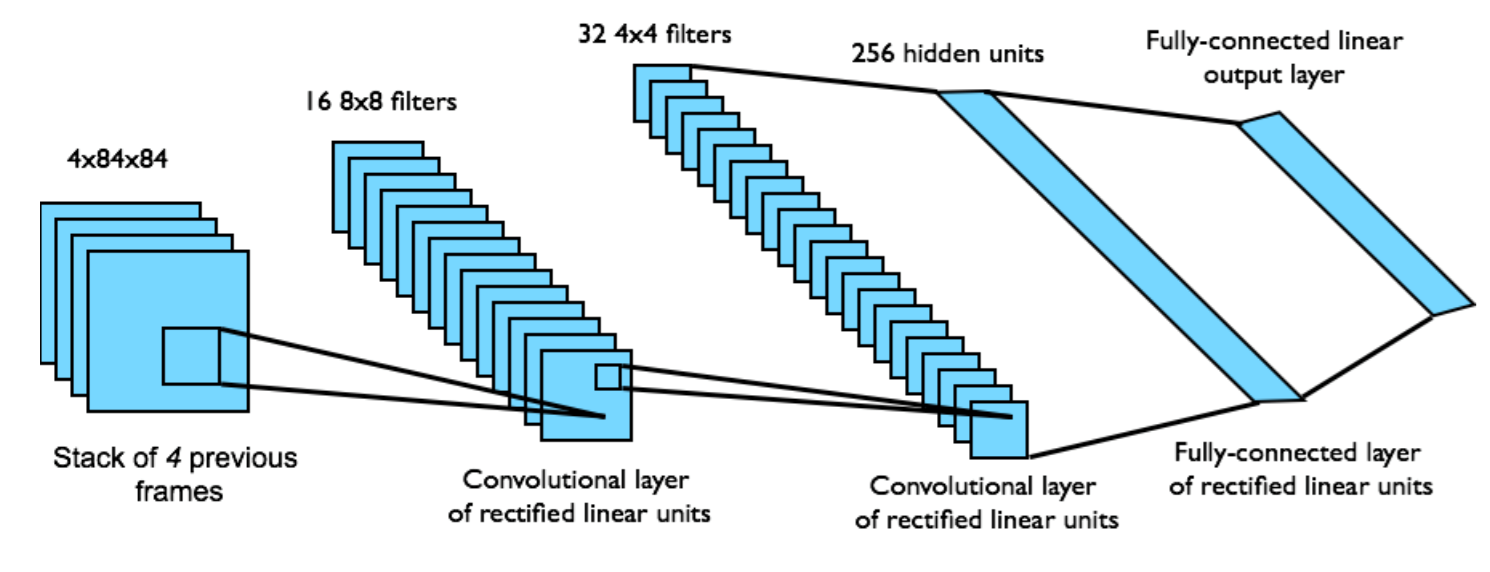
이 모델은 $Q^*$를 단 한번의 forward pass만으로 구할 수 있다는 장점이 있습니다.

  • input: $\phi(s_t)$

  • ouput: 가능한 모든 action에 대한 Q-value (4~18)

  • reward: (1,0,-1) 값으로 고정

  • RMSProp algorithm with minibatches of size 32

  • $\varepsilon$-greedy policy: $\varepsilon$ = 1 to 0.1 (~백만), $\varepsilon$ = 0.1 (o.w)

  • a simple frame-skipping technique (agent가 on every kth frame에만 action을 선택)

논문에서 주목할만한 4가지 contribution

  1. raw pixel을 받아와 directly input data로 다룬 것

  2. CNN을 function approximator로 이용한 것

  3. 하나의 agent가 여러 종류의 Atari game을 학습할 수 있는 능력을 갖춘 것

  4. Experience replay를 사용하여 data efficiency를 향상한 것

Previous강화학습 (Reinforcement Learning)NextReinforcement Learning(2)

Last updated